[Neirdan]

Je connais le point A et le point B, je souhaite placer un cercle (2D - en rouge) sur la tangente (au point B donc), il faut donc que je calcule sa rotation.
Je pars d'un cercle défini en X Z (Y étant la hauteur).

Pas réussi à trouver quoi que ce soit de concluant sur le net que ce soit en français ou anglais.
Edit: apparemment je pourrais me servir de AB comme de la normale et récupérer le plan, mais toujours pas trouvé de formule.

[FLloyd]

Euh, ton point B, il est sur un Rayon du cercle là non...?

Tu dois avoir mal formulé ton problème parce que je comprend pas ce que tu veux en fait.(Bon ça fait 24h que j'ai pas dormi, c'est ptét moi...)

[Gofyk]

c'est pas clair ton affaire ou alors j'ai pas assez dormi. tu parles de 3D donc sur ton premier schéma c'est une sphère?

[Sergul]

Bah tu as un vecteur AB, donc trouve un vecteur perpendiculaire à AB, puis joue avec sa norme (taille) pour qu'elle soit égale au rayon du cercle voulu. Pour se représenter la chose, il suffit du centre et du vecteur que tu vas faire tourner autour.

Sinon autre méthode c'est de prendre l'équation de la sphère de centre B et de rayon voulu (pas précisé sur ton schéma donc je suppose que tu le connais), et l'équation du plan perpendiculaire à AB passant par B. A partir de ces deux équations tu trouves logiquement celle de ton cercle, puisque c'est l'intersection entre les deux.

[Thorkas]

Question : tu parles d'un cercle ou d'une sphère ?

Si tu parles d'une sphère, tu cherches bien le plan tangent ? ("la" tangente, c'est à une courbe, "1D", une surface aura un plans tangents). Auquel cas Sergul à répondu.

Sinon va falloir préciser

[Rafa]

J'ai pas compris le coup de "calculer sa rotation".

Si c'est les points du cercle que tu veux, faut faire l'intersection entre la sphère centrée en B avec le rayon de ton cercle (l'équation est triviale), et le plan tangent en B à ta grande sphère (équation normalement triviale aussi, t'as un vecteur normal et un point). Et t'as plus qu'à t'amuser avec ton système non linéaire de 2 équations.

[Sergul]

Bah s'il cherche une sphère c'est encore plus simple, y'a même pas besoin de chercher l'intersection avec le plan.

[Neirdan]

Oulà effectivement j'étais un peu perché hier moi aussi à cause de la fatigue.

Alors:
Je parle d'une sphère. Pour un cercle ça aurait été facile car il n'existe qu'une perpendiculaire à AB passant par B.
Important à noter: ce que je cherche à faire, c'est une rotation sur l'angle X, une sur l'angle Y et une sur Z pour que mon cercle soit positionné comme sur l'image de base (en rouge).
Ce cercle, par défaut, est de rotation 0,0,0 et est tracé selon l'axe XZ (donc sur XY et YZ, ça donne un trait).

Le problème en géométrie 3D c'est que trouver la normale d'un plan c'est easy, y'a le produit vectoriel pour ça. Et pour trouver un angle, y'a le produit scalaire. Et je n'arrive pas à trouver de solution en utilisant ces 2 trucs que je connais.
Pour info, je n'ai encore jamais vraiment utilisé les angles d'euler et je ne sais pas si c'est une solution ou non.

[Sergul]

Mais explique ce que sont l'angle X, Y et Z, parce que ça veut RIEN dire. X, y et z sont des axes, ou selon le contexte les coordonnées sur ces axes. D'ailleurs, faire une rotation SUR un angle, ça me parle juste pas. Faire une rotation d'angle alpha je vois bien, mais une rotation SUR l'angle alpha, euh, lolwut ?

C'est vraiment mal expliqué, refais un schéma qui explique tes x, y et z stp. Définis clairement les termes que tu utilises : quel élément est un point, un plan, une droite, un vecteur, un cercle, ou une sphère, etc.

[kermo]

Il te faudra à mon avis passer par les angles d'Euler, mais comme dit au-dessus, éclaircis un peu tes notations parce que l'axe XY ou l'angle Z c'est difficile de comprendre ce que ça veut dire.

On peut trouver la rotation à appliquer à un cercle donné pour qu'il se retrouve centré sur le point B. Mais je ne suis pas sûr que ça soit ça que tu cherches vraiment ?

[leZilou]

En gros tu cherches les coordonnées polaires de B.

[Chernish]

Déjà, il suffit de deux angles pour atteindre tout point sur une sphère. Pense à latitude et longitude. Ton 3ème angle ne sert à rien.

Soit
- un repère orthonormé d'axes x,y,z avec x la largeur, y la hauteur et z la profondeur
- une sphère de centre A et de rayon R
- un point B sur la surface de cette sphère, déterminé par l'angle béta par rapport au plan xz (le plan horizontal) et l'angle alpha par rapport au plan xy (le plan vertical)

Trouver l'expression du cercle de rayon r de centre B et de plan tangent à la sphère.

En coordonnées cartésiennes, le point B est donné par: Bx=Ax+R*cos(alpha)*cos(béta), By=Ay+R*sin(alpha), Bz=Az+R*cos(alpha)*sin(béta)
On y arrive par simple projection dans les plans.

Expression du plan tangent: l'ensemble de points P tels que AB.BP=0
Expression de la sphère de rayon r centrée en B: l'ensemble de points P tels que ||BP||=r

Donc ton cercle est donné par l'ensemble des point P tels que AB.BP=0 et ||BP||=r

[Neirdan]

Une image vaut mieux qu'un long discours.

Ce que j'appelle faire une rotation sur X, c'est faire une rotation selon l'axe X.
Faut pas faire gaffe au fait que Y et Z soient inversés en vue 3D, c'est juste une question de point de vue.

Le résultat que je cherche à obtenir, c'est la rotation du cercle pour qu'il soit sur le plan tangent à la sphère au point de contact entre les deux (B sur le premier dessin)

[Korteks]

En fait tu étudies l'Etoile Noire

Sergul a répondu à la question de base, mais là je comprends vraiment pas ton histoire de rotation. Tu parle d'une rotation sur l'axe X, mais tel que dessiné je comprends qu'il s'agit de la rotation de la sphère, mais ensuite tu parle de rotation du cercle (ce qui ne changerait pas grand chose : il peut tourner autant qu'il veut, son centre ne bougera pas...);

Mon interprétation de ta photo : le cercle est déjà présent (sur un axe tangent à la sphère), la sphère tourne sur elle-même selon un axe unique (rotation simple) et tu voudrait calculer à quel moment le centre du cercle atteindrait un point donné ?
Parce qu'autrement, en lisant ton message d'origine, je ne comprends pas bien ce que vient faire cette histoire de rotation dans l'affaire, s'il s'agit juste de placer un cercle au point B... :/

[Kam']

Mais comment ça tu veux obtenir la rotation du cercle pour qu'il soit tangent à la sphère?

Citation :

Publié par Kam'

Mais comment ça tu veux obtenir la rotation du cercle pour qu'il soit tangent à la sphère?

Oui pourquoi vouloir une rotation ?
Tu crée un cercle tel qu'il soit sur un plan normal à AB passant par B (très facile à écrire avec le vecteur normal)
Tu dis que la distance de M à B doit être inférieure à R.
Sinon en paramétrique :
Tu trouves deux vecteurs orthogonaux à AB (par exemple tu trouves le premier vecteur en faisant une disjonction des cas* et tu fais un produit vectoriel pour trouver le troisième, tu as donc BC et BD base de ton plan tangent) puis tu fais tourner et bouger ton point :
Le disque est paramétré par r(cos t BC + sin t BD) où r et t varient comme il faut. (Et tu peux discrétiser ça aussi)

Pour trouver algorithmiquement un vecteur normal à un autre tu peux faire : si (a,b,c) non colinéaire à (1,0,0) tu prends le produit vectoriel (normé) entre les deux. Si (a,b,c) colinéaire à (1,0,0) tu prends (0,1,0)

[Sergul]

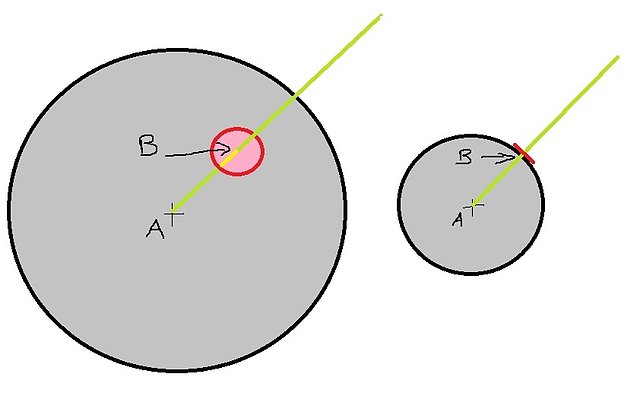
En gros tu veux un cercle de centre B qui soit sur le plan tangent à la grande sphère au point B, c'est bien ça ? Si c'est ça alors c'est exactement ce que j'ai dis : Tu prends l'équation de la petite sphère de centre B et de rayon R (que tu n'as jamais précisé) et l'équation du plan, et l'équation de ton cercle en est l'intersection (le fait de passer par une petite sphère, je fais ça pour simplifier car je ne connais pas l'équation d'un cercle dans l'espace, je suis même pas sûr qu'il y ait une équation cartésienne pour ça d'ailleurs, à check).

Pour dire ça autrement, ton cercle c'est l'ensemble des points qui satisfont à la fois l'équation du plan et celle de la petite sphère de rayon R. Encore autrement dit, tu poses equationDePetiteSphere = equationDePlanTangentEnB, tu simplifies le système et tu obtiens l'équation de ton cercle.

Maintenant, si tu veux que ta sphère tourne, la seule chose qui change c'est ton point B (et donc ton vecteur AB). Du coup, dynamiquement, tu remplaces ça dans les formules et c'est gagné.

Tu as comme équations :
La grande sphère " S " : (x-a)² + (y-b)² + (z-c)²-R² = 0 avec (a,b,c) son centre, et R son rayon (celui de la grande sphère, donc).

Le plan tangent à la sphère en B " Pi " : ax + by + cz + d = 0 avec (a,b,c) les composantes du vecteur AB, et d qui en est déduit sachant que Pi passe par B (et gaffe, a b et c ne SONT PAS LES MEMES que dans l'équation de " S " !!! Flemme de changer les lettres)

La petite sphère " s " : (x-a)² + (y-b)² + (z-c)²-R² = 0 avec (a,b,c) les coordonnées du point B, et avec R le rayon du cercle que tu cherches

Tu poses s = Pi et tu résous, ça te donnera l'équation de " c ", ton cercle. J'vais pas trop te mâcher le travail, je te laisse le soin de le faire.


Maintenant j'ai toujours pas compris ton histoire de rotation, mais d'une manière générale, tu as A le centre de la grande sphère, B un point sur la grande sphère. Admettons que tu trouves un point B' sur cette sphère, par rotation, eh bien pour trouver l'angle entre B et B' par rapport à A, tu prends les vecteur AB et AB', et grâce au produit scalaire tu en trouves l'angle.
alpha = Arccos((AB*AB')/(||AB||*||AB'||))

[Rafa]

En gros tu cherches la distance angulaire entre 2 points (B, et le centre de ton cercle "avant rotation", qu'on appellera par exemple C) ? Si c'est le cas il y a le passage en coordonnées sphériques (ce que décrivait Chernish) qui ferait l'affaire...

Normalement rien qu'avec le centre et le fait que ce soit tangent, tu devrais pouvoir refaire tout ton cercle.

Mais je suis toujours incertain de ce que tu veux vraiment. Comme quoi un long discours vaut parfois plus qu'une image. Genre ça pourrait aussi très bien être une rotation sur lui-même d'un cercle déjà en B pour passer d'une position non-tangente à une position tangente... Bref, pas sorti de l'auberge
'fin bref, si tu parles de rotation, c'est que t'as une position de départ et d'arrivée. Jusqu'ici j'en ai pas vu la mention.

[Neirdan]

Parce qu'on est en développement 3D et que j'utilise une fonciton de génération d'un mesh (objet 3D formé de vertices et indices).

Donc le mesh que je génère, le centre est en 0,0,0 et mes points sont en XZ avec Y toujours égal à 0.
Du coup, si ce mesh est au pôle nord, aucun problème de rotation.

Edit: oui, c'est une rotation sur lui même, et le mesh est déjà positionné en B.
Du coup, effectivement, faire une rotation sur Z ne sert à rien vu que cela ne fera que tourner le cercle sur son axe central.

[Sergul]

J'ai édité mon précédent message, ça correspond à ce que tu cherches ?

Edit : Ah tu veux que ton cercle tourne sur lui-même ? Ca veut dire que de base il a un sens, ce qui n'est pas inclut dans la définition mathématique d'un cercle il me semble. Je pense qu'il te faut dans ce cas définir un "point P" sur ton cercle, et le faire tourner, ce point P serait le point de "départ" de l'image, un point de référence sur le cercle. Ce point est accessible par son vecteur OP = OB + BP.

Et du coup, tu effectues ta rotation sur BP, ce qui te donne à chaque fois un nouveau OP.

C'est compréhensible ? Si oui, j'suis bon ou à côté de la plaque ?

[Rafa]

Citation :

Publié par Neirdan

Parce qu'on est en développement 3D et que j'utilise une fonciton de génération d'un mesh (objet 3D formé de vertices et indices).

Donc le mesh que je génère, le centre est en 0,0,0 et mes points sont en XZ avec Y toujours égal à 0.
Du coup, si ce mesh est au pôle nord, aucun problème de rotation.

Edit: oui, c'est une rotation sur lui même, et le mesh est déjà positionné en B.
Du coup, effectivement, faire une rotation sur Z ne sert à rien vu que cela ne fera que tourner le cercle sur son axe central.

Jamais fait de dev 3D. Ton "mesh", tu peux lui faire faire des translations et rotations, et donc tu veux savoir quels params utiliser dans ton cas ? (la translation étant obvious, reste les params d'angle de la rotation...).
Si c'est ça, à mon avis si tu exprimes ton vecteur AB en coordonées sphériques avec la convention rayon-colatitude-longitude, tu as directement tes angles nécessaires (grosso modo tu aurais les angles de rotation du vecteur normal Oy du mesh initial vers le vecteur AB, et la rotation du vecteur normal c'est la même que celle du cercle)

[MoaYs]

Le problème m'a l'air plan, Geometrie 3D étant une logiciels de géométrie .
( ce logiciel, si je m'abuses, peut faire bouger les figures 2D donnant l'illusion 3D )

Il n'y a pas suffisamment de données pour conclure,
le mieux étant de posté l'exercice original ( scan -> jpeg etc ...)
J'ai déjà eu un problème similaire avec un exercice mal posé où chacun voyait midi à sa porte
Parmi toutes vos suggestions , je note celle des angles d'Euler

[Neirdan]

Citation :

Publié par MoaYs

Le problème m'a l'air plan, Geometrie 3D étant une logiciels de géométrie .
( ce logiciel, si je m'abuses, peut faire bouger les figures 2D donnant l'illusion 3D )

Il n'y a pas suffisamment de données pour conclure,
le mieux étant de posté l'exercice original ( scan -> jpeg etc ...)
J'ai déjà eu un problème similaire avec un exercice mal posé où chacun voyait midi à sa porte

Je n'ai pas d'autre réaction.

Géométrie 3D n'est ni un ni une logiciel de 3D, les screens d'exemple proviennent de blender.
Mis à part ça, je développe sous Irrlicht (un render engine 3D).
C'est pas pour l'école, c'est pour un projet de jeu vidéo amateur.

[Sergul]

Citation :

Publié par Neirdan

Je n'ai pas d'autre réaction.

Géométrie 3D n'est ni un ni une logiciel de 3D, les screens d'exemple proviennent de blender.
Mis à part ça, je développe sous Irrlicht (un render engine 3D).
C'est pas pour l'école, c'est pour un projet de jeu vidéo amateur.

Vu la donnée de base j'ai l'impression que mes réponses conviennent, mais comme j'ai rien compris à tes réponses j'ai l'impression d'être à côté de la plaque. C'est le cas ?

J'avoue que je comprends toujours absolument rien de ce que tu cherches à faire, si ce n'est pas trouver l'équation d'un cercle tangent à une sphère

[Neirdan]

Je suis en train de coder, je posterai le résultat final et la méthode que j'aurai utilisé et si ca marche ou non