Publié par Kor Ae'Reen
Si. Pourquoi tu dis après que c'est égal à x +4 ça c'est parce que c'est pareil ok. Mais comment on sait combien de fois on doit mettre pour trouver la bonne solution ? Ca pourrait être x + 2TT ou + 6TT comment je sais ?
Quand on te demande de trouve la solution de cos(x)=0.4, par exemple, tu as une infinité de solutions.
Si ta prof t'en demande une en particulier, elle te precisera l'intervalle sur lequel tu dois trouver ta definition (comme dans ton exo, ou tu dois trouver LA solution sur [Pi,2PI] : dans ce cas la, la solution est unique).
Publié par Kor Ae'Reen
Sinon je ne comprends pas l'entier relatif k. Pourquoi le mettre ? On rajoute 2TT ou 4TT, mais c'est quoi le k de 2*k*TT ?
Le k, c'est juste une notation un peu plus facile.
au lieu d'ecrire 1.16, 1.16+1*2PI, 1.16-2PI, 1.16+2*2PI, 1.16-2*2PI etc etc, on ecrit 1.16+k*2PI, ou k est un entier relatif, c'est a dire ou k peut valoir 0, 1, -1, 2, -2, 3, -3 etc.
Publié par Kor Ae'Reen
Comment trouve-t-ton le -2Pi/3 ou 2Pi/3 ? C'est une valeur remarquable ou non ? Quand c'est pas une valeur remarquable, comment trouver x ?
Oui, le 2Pi/3, c'est une valeur remarquable. Il y en a pas beaucoup a connaitre, mais les savoir simplifie bien la vie.
Pour les valeurs non remarquables, le plus simple est ou bien de le faire garphiquement, ou bien d'utiliser une calculatrice (beaucoup ont une touche cos^-1), mais ca ne te donnera pas une solution exacte.
Autrement, on peut approcher la solution, mais aucune de simple dans mon souvenir. Je pense que si ta prof veut que vous trouviez a la main une solution approximative, elle detaillera les questions
Publié par Kor Ae'Reen
En fait, dans ce cercle donc, je le fais normal de 0 à TT disons, et comme mon intervalle c'est [TT;2TT], bah je rajoute 2TT ?
Si ça avait été [2TT;4TT], j'aurais juste rajouté 4TT en plus à mon nombre ?
C'est presque ca, mais pas tout a fait

Si tu trouves ta solution dans [0,Pi] et que tu rajoutes 2Pi, tu vas tomber dans [2Pi,3Pi], donc en dehors de l'intervalle ou tu travailles.
Ce qu'il ne faut pas oublier, c'est que tu as deux solutions : une sur [0,Pi] (graphiquement, celle du haut du cercle trigo) et celle sur [-Pi,0] (graphiquement, celle du bas).
Si tu veux une solution sur [Pi,2Pi], il faut que tu ajoutes 2Pi a la solution qui se trouvait dans [-Pi,0].
Et si ca avait été [2Pi,4Pi], il y aurait eu un probleme, car il y a deux solutions sur [2Pi,4Pi] ("celle du haut+2Pi" et "celle du bas+4Pi").
(En gros, pour avoir une solution unique, il faut travailler sur un segment de longueur Pi)
Grumpf, j'ai le sentiment de ne pas avoir ete clair a la fin (sommeil moi ^^) mais j'espere que ca aidera


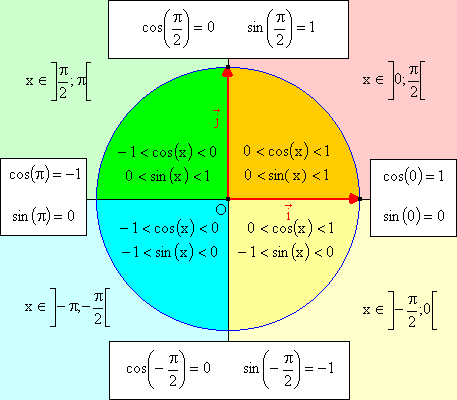






 )
)
 )
)