| Zangdar MortPartout |
| Voir le profil public |
| Trouver plus de messages par Zangdar MortPartout |
| Aller à la page... |
Calcul loi binomiale
| Suivre Répondre |
|
|
Partager | Rechercher |
|
|
pas moyen par excel ?
|
|
|
|
|
|
Probablement mais un truc tout fait m'arrangerait, j'ai pas vraiment le temps de refaire la formule sur papier avant de la rentrer sous excel
|
|
|
|
| Zangdar MortPartout |
| Voir le profil public |
| Trouver plus de messages par Zangdar MortPartout |
|
|
Je te conseillerai bien R (un logiciel de stat) mais c'est sans doute un peu lourd pour si peu.
 La proba de succes p est de 0.01. C'est un simple tirage aléatoire avec remise. Tu fais l'experience 1 fois, tu as : 0.01 * 1 = 0.01 chance de succès. Tu fais l'experience 2 fois, tu as : 0.01 * 2 = 0.02 chance de succès. Tu fais l'experience 10 fois, tu as : 0.01 * 10 = 0.1 chance de succès (un chance sur 10). Tu fais l'experience 50 fois, tu as : 0.01 * 50 = 0.5 chance de succès, soit une chance sur 2. |
|
|
|
|
|
Citation :
        Si tu fais n tirage, la probabilité d'avoir une réussite (ou plus) est 1-(0,99)^n. |
|
|
|
|
|
|
|
|
|
|
|
Citation :
Ah non ça marche pas comme ça justement Citation :
 Edit: ça colle pas, l'équation qui donne n sort du domaine du logarithme |
|
|
|
| Zangdar MortPartout |
| Voir le profil public |
| Trouver plus de messages par Zangdar MortPartout |
|
|
C'est exactement cela, et ça fait 68,96756...
Donc 69 essais =) jol n'a pas vocation à vous aider à faire vos devoirs 
|
|
|
|
|
|
Pas besoin de machine donc. C'est beau le cerveau humain.
|
|
|
|
|
#220547
Invité
|
Sinon, tu peux utiliser la vraie formule avec trois facteurs :
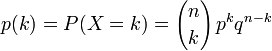 Tu l'as appliquée pour X=0 très facilement, ca fait 0.99^n |
|
|
| #220547 |
| Zangdar MortPartout |
| Voir le profil public |
| Trouver plus de messages par Zangdar MortPartout |
| Suivre Répondre |
Fil d'ariane
Connectés sur ce fil1 connecté (0 membre et 1 invité)
Afficher la liste détaillée des connectés
|


